Логика
Сейчас идет \(2019\)-й год, и в его записи все цифры различны. Найдите ближайший год будущего, в записи которого снова все цифры будут различны.
Во-первых, нетрудно убедиться, что указанный год подходит. Далее, если год ближе, то это либо год \(2030\) (и в нем два нуля), либо год вида \(202\star\), и в нем две двойки. Значит, никакой более близкий год не походит, а \(2031\)-й год подходит. Поэтому он и является ближайшим.
Ответ: 2031.
У Гарри Поттера носки хранятся в большом сундуке, который ему тяжело открывать. Поэтому он достает носки на ощупь, не глядя на их цвет. Всего у Гарри по \(10\) носков трех цветов: красного, желтого и черного. Какое наименьшее количество носков ему нужно вытащить, чтобы среди них обязательно нашлась пара одноцветных?
Сначала отметим, что если Гарри вытащил \(4\) носка, то среди них обязательно найдется пара одноцветных. В самом деле, предположим противное, то есть что пары одноцветных носков у него не нашлось. Тогда все \(4\) носка разного цвета, а значит и цветов хотя бы \(4\). Но по условию у Гарри носки бывают только трех цветов, противоречие. Значит, \(4\) носков Гарри хватит.
Покажем, что меньшего количества носков ему может не хватить. Если он вытащил \(3\) или меньше носков, то они могут быть все три разных цветов: первый вытащенный красный, второй — желтый, третий — черный.
Таким образом, \(4\) носков точно хватит, а вот меньшего количества может и не хватить. Значит, ответ в этой задаче \(4\) носка.
Ответ: 4 носка.
Какое наибольшее число трехклеточных уголков можно вырезать из шахматной доски \(8\times 8\)?
Всего в шахматной дочке \(8\times 8\) \(64\) клетки. Поэтому больше \(21\) уголка вырезать нельзя, так как если мы вырежем хотя бы \(22\) уголка, то на них уйдет не меньше \(22\cdot 3=66\) клеток, а такого количества клеток на шахматной доске нет.
Теперь покажем, как вырезать \(21\) уголок. Вырежем один уголок из нижнего правого углового квадрата \(2\times 2\), а оставшуюся часть доски разобьем на \(10\) прямоугольников \(3\times 2\) так, как показано на рисунке.
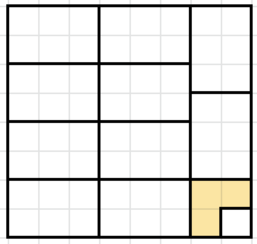
Каждый такой прямоугольник \(3\times 2\) можно разбить на два уголка. Всего получился \(10\cdot 2+1=21\) уголок, значит, мы построили один из возможных примеров, как можно вырезать \(21\) уголок.
Таким образом, мы показали, что вырезать больше, чем \(21\) уголок, нельзя, и привели пример, как можно вырезать \(21\) уголок. Значит, наибольшее число трехклеточных уголков, которое можно вырезать из шахматной доски \(8\times 8\), равно \(21\).
Ответ: 21 уголок.
Найдите ближайший в будущем год, в записи которого не встречается цифра \(0\).
Ответ:
Даны \(20\) различных натуральных чисел. Известно, что сумма любых двух из них делится на \(10\). Какое наименьшее количество чисел, делящихся на \(10\), может быть среди них?
Ответ:
Какое наибольшее количество чисел Гермиона может написать на доске так, чтобы сумма любых двух чисел была нечетной?
Ответ:
У Гарри Поттера носки хранятся в большом сундуке, который ему тяжело открывать. Поэтому он достает носки на ощупь, не глядя на их цвет. Всего у Гарри по \(10\) носков трех цветов: красного, желтого и черного. Какое наименьшее количество носков ему нужно вытащить, чтобы среди них обязательно нашлась пара красных?
Ответ:
