Геометрия
Можно ли разрезать квадрат \(4\times 4\) по клеточкам на три фигуры равной площади?
Заметим, что суммарная площадь трех фигурок должна быть равна площади исходного квадрата. А так как разрезание должно быть проведено по клеточкам, то фигуры получатся с целой площадью. Поэтому, если площади фигурок будут равны, то их суммарная площадь будет делиться на \(3\). Но \(16\) не делится на \(3\), значит, такого разрезания не существует.
Ответ: Нет, нельзя.
Можно ли разрезать квадрат \(4\times 4\) по клеточкам на три фигуры равного периметра?
Пример такого разрезания указан на рисунке.
Комментарий. Можно заметить, что каждую фигурку без изменения периметра можно дополнить до прямоугольника \(4\times 2\). То есть периметр каждой фигурки равен периметру прямоугольника \(4\times 2\), поэтому совершенно не удивительно, что эти периметры равны. Из этих соображений можно достаточно часто строить примеры необычных фигурок фиксированного периметра.
Ответ: Да, можно.
У Джуди и Ника есть по одному клетчатому прямоугольнику. Может ли оказаться, что периметр больше у прямоугольника Джуди, но площадь — у прямоугольника Ника?
Пусть у Джуди прямоугольник имеет размеры \(1\times 10\), а у Ника — \(4\times 4\). Сравниваем периметры: \[2\cdot (1+10) =22> 2\cdot (4+4)=16.\]
А если сравнить площади, то \[1\cdot 10=10< 4\cdot 4=16,\] то есть два таких прямоугольника подходят под условие.
Комментарий. Разумеется, для полного решения этой задачи достаточно привести любой пример, коих множество. Не смущайтесь, что у Ника в данном примере квадрат — квадрат тоже является прямоугольником.
Ответ: Да, может.
У Джуди и Ника есть по одному одинаковому клетчатому квадратику. Джуди разрезала его по клеткам на три одинаковые части, а Ник — на четыре одинаковые части. Могут ли площади фигурок Джуди и Ника оказаться равны?
Заметим, что так как фигурки у Джуди равны, то равны и их площади. При этом в сумме площади трех фигурок дают площадь исходного квадрата, значит, площадь каждой фигурки Джуди составляет треть площади исходного квадрата. По тем же рассуждениям площадь каждой фигурки Ника составляет четверть площади исходного квадрата. Но треть площади не может быть равна четверти той же самой площади, значит, площади фигурок Джуди и Ника не могут оказаться равны.
Ответ: Нет, не могут.
Мисс Барашкис отрезала от квадрата \(4\times 4\) один угловой квадратик. Помогите ей разрезать оставшуюся фигурку на \(5\) равных частей, не являющихся прямоугольниками.
Возможный пример разрезания указан на рисунке.
Как до него догадаться? Предварительно можно посчитать, что от квадратика остается \(16-1=15\) клеток, и раз надо разрезать на \(5\) фигур, то каждая фигурка состоит из \(15:5=3\) клеток. А так как фигурки не должны являться прямоугольниками, то остается только уголок из трех клеток, и как раз на эти уголки мы и режем.
Ответ:
У Мисс Барашкис есть клетчатый квадрат \(8\times 8\), а также клетчатый квадрат \(6\times 6\). Помогите ей разрезать каждый квадрат по клеточкам на две части так, чтобы из 4 полученных частей можно было составить квадрат \(10\times 10\).
Сначала подумаем, что же будет полным решением этой задачи? Надо, во-первых, разбить два квадрата на две части. Кроме этого, надо также показать, как из 4 частей сложить квадрат \(10\times 10\). Это мы в итоге и сделаем, но сначала пару слов о том, как придумать такой пример.
Расположим имеющиеся квадраты \(8\times 8\) и \(6\times 6\), не разрезая их, так, чтобы они вписались в квадрат \(10\times 10\), естественно, накладываясь друг на друга:
Теперь уже видно, как можно получить искомое разрезание: надо накладывающуюся друг на друга часть переложить на два пустых участка. Для этого отрежем по прямоугольнику \(2\times 4\) от каждого из квадратов так, чтобы в итоге оставшиеся части квадратов не пересекались, например, так:
В итоге квадрат \(10\times 10\) мы сможем сложить так:
Ответ:
У Джуди и Ника есть по одному одинаковому клетчатому квадратику. Джуди разрезала его по клеткам на три одинаковые части, а Ник — на четыре одинаковые части. Могут ли периметры фигурки Джуди и фигурки Ника оказаться равны?
Разумеется, так как наш ответ “могут”, достаточно лишь привести пример. Но мы также расскажем, как до этого примера можно додуматься, с чего и начнем.
Во-первых, квадратик должен резаться по клеточкам как на \(3\), так и на \(4\) части. Это как минимум означает, что его площадь должна делиться и на \(3\), и на \(4\). Поэтому для удобства возьмем квадратик \(6\times 6\). Еще раз, никто нас не заставляет брать именно такой квадратик, более того, если с ним ничего не получится, это еще не будет означать, что такого разрезания в принципе не существует. Просто такой квадратик “удобнее”.
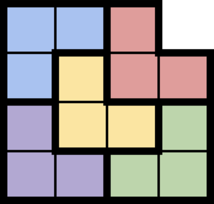
Продолжаем рассуждать дальше. Вообще, обычно чем меньше площадь фигурки, тем меньше и ее площадь, хоть и не всегда. Поэтому на месте Джуди разрежем квадратик на три части как можно меньшего периметра: на три прямоугольника \(6\times 2\).
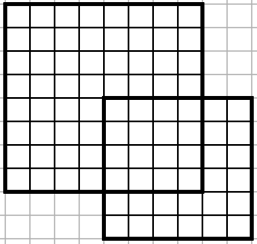
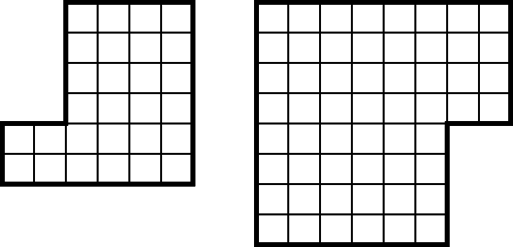
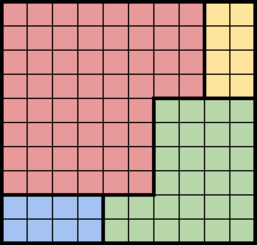
Теперь Нику надо разрезать этот же квадратик на \(4\) фигурки периметра \(2\cdot (6+2)=16\). Это можно сделать, например, так:
Легко убедиться, что два таких разрезания квадрата \(6\times 6\) подходят под условие. Таким образом, периметр фигурки Джуди мог оказаться равным периметру фигурки Ника.
Ответ: Да, могут.
